【为了让不同程度的使用者包括初学者也可以阅读这篇文章。本文使用的范例程序结构简单但足够典型。着重于介绍思路的分析,反映设计过程中遇到的数据处理及如何解决问题的思维过程。对涉及的工具就使用不做细致的介绍,敬请见谅—Dixon】
在使用参数化设计工具辅助设计的过程中用户需要解决两个阶段的问题:
- 根据设计要求规划合理的编程逻辑顺序。(编程思维过程)
- 使用参数化设计工具实现设计功能。(技术处理过程)
在这几年接触学习参数化设计的学员的过程中,我们发现大部分学员会在这两个阶段遇到不同的问题。
其中,第一个阶段属于使用者编程思维方式主导的部分。由于大部分设计背景的学员之前并没有接受过系统的编程课程的训练,因此普偏在编程逻辑思维方面较为欠缺。本文的范例中对实际的设计要求有简单的编程逻辑思维方法的解释可作为参考。
第二个阶段属于技术细节的部分。我们注意到大部分GH用户遇到的技术细节问题可以归类于以下三方面:
1.对GH的工具的运行原理和使用方法不够理解。这是比较初级的问题。
2对GH工具涉及到的曲面造型技术缺乏足够了解。具体为:对Nurbs的几何特性、Nurbs数据的编程控制方法和曲面造型思路缺乏了解。因此程序中涉及曲线曲面控制处理的部分较难深入和灵活运用。这部分较为欠缺的用户建议可以参加rhino原厂开设的曲面造型课程的短期学习班做系统的补充。
3.除了以上两个参见的问题之外,大部分学员都会在学习到一个阶段后遇到GH树形据结构数据管理的理解和控制方面的困难。这通常是所有学习GH者都需要跨过的一道坎。
和其他的参数化设计软件和编程软件不同,GH采用的树形据结构的数据管理是很特别的,,它可以让用户更容易的管理和控制庞大和复杂的数据,以实现用参数化控制复杂的功能甚至是系统的设计(如一整栋建筑),但前提是使用者必须对这种数据管理和控制的原理有对应的了解,才能对其进行合理和灵活的控制。这部分是很多人学习中遇到的难点或者难以深入到的部分。
为了帮助GH使用者GH的理解树形数据结构在参数化设计过程中起到的作用,以及如何配合设计需求处理和控制它,我们使用GH原厂课程中的一个范例来做介绍。
我要设计一座悬挂结构的桥!
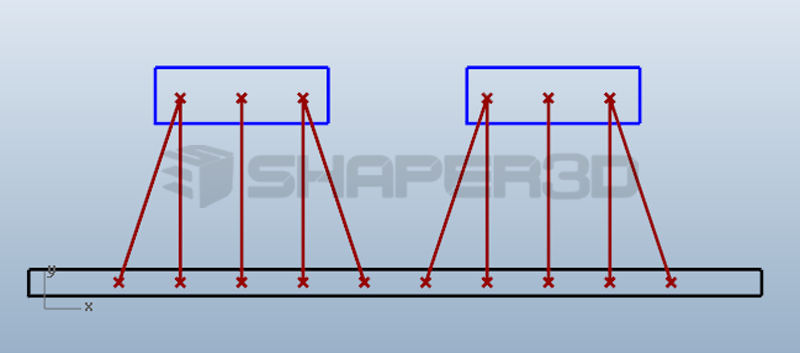
这是一个悬挂结构的桥,如图是整个桥的侧面结构。黑色矩形方框是桥体。桥体上10个红色点桥体的固定点。用钢丝悬挂固定。顶上的两个蓝色矩形代表悬挂桥的两个立柱,每个立柱上各有3个钢丝固定点。我们需要解决的问题就是如何在桥体和柱子的固定点之间拉钢丝。
这个设计中遇到的实际问题可以被简化为点连线的问题,即:
如何在下面10个点和上面6个点(2*3结构)之间做各种连线方式的设计。
为了理清设计思路,我们先看两种最极端的连线方式:
1.最稳固的方式(连线最复杂)
2.和最省材料的方式(连线最简单)
最稳固的连线方式(连线最复杂)
所谓最稳固的方式(并且是合理的),也即是:
桥体的每个点(地下的10个)都和柱子上的每个点(顶上的6个)都做连线
这个连线方式题就可以简化为:10个点和6个点之间的连线组合,很明显会有60条线(10*6)。
虽说是最复杂的连线方式,但是在编程逻辑中却是最简单的,程序如下图:

为了集中表述问题的关键部分,图片中去掉了点生成的程序部分。
在程序处理细节方面注意line工具的内部必须切换成cross的数据对应方式,这在程序外部看不出来。
连接效果如图:
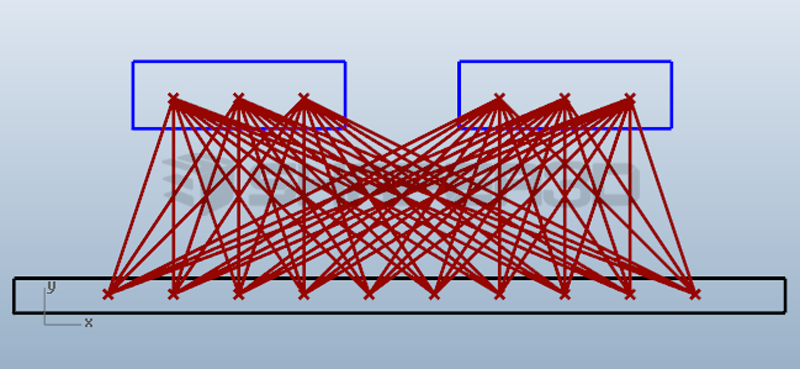
虽然这是最稳固的连接方式,逻辑上来讲很简单,程序处理也很容易。但连接的视觉效果却不够好,因为桥体每个点都有6跟连线,因此连线过于密集(60根连线),造价也较贵(很多更多钢缆)。
最省材料的方式(连线最简单)
再来看最省材料的连接方式:
即:桥体上的每个点(10个点)只使用一根钢丝做固定。从连接的角度可以理解为:
底部的10个点每个点都和上面的6个点的其中之一做连接。
那么具体和顶部的哪一个点做连接呢?我认为和最近的一个点连接是最合理的,因为最省材料而且钢缆牵引的角度也更趋近于垂直向上,力学上来说较为合理。 所以,整个连线的逻辑就是:
底部的10个点中每个点与顶上的6个点中最近的一个点做连线。
这个逻辑就稍微复杂一点了,从编程逻辑考虑实现这个效果可以分为两个步骤实现:
1.首先分别做出底部的每个点和顶上6个点的连线。
2.然后从每个底部点的6个连线中挑选出最短的一根。
在这个编程逻辑中要特别注意:第一步骤的程序输出的数据是有结构分支做管理的,因为第一步实际上仍然是得到60根线(10个点其中每个点6根线),但是如果这60根线是混在一起的,那么在第二步骤中就无法找出属于某一点的6根连线,因此也无法完成第二个步骤中规划的逻辑效果。因此这60跟线应该是依据底部的10个点来做分支处理的,也即是:第一步输出的数据结构应该包含有10个分支,对应的是底部的10个点,而每个分支里面有6个数据,代表连接到某个点的6根线。这种数据结构可以反映60跟线中那些线是连接那个点的,数据结构图和GH中的Param Viewer观察输出结构应该如下图所示:
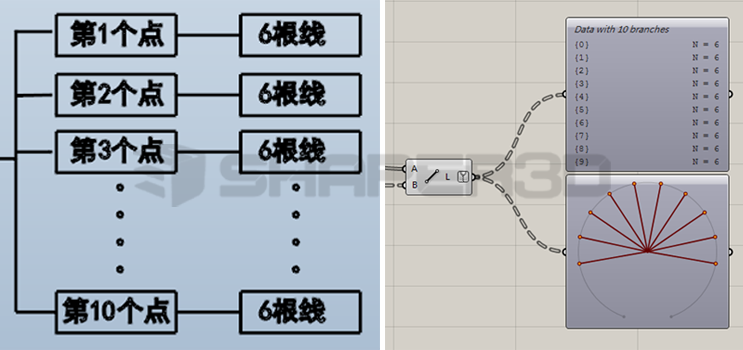
Param Viewer是用于检查树形结构常用的工具,用户应该熟悉如何去阅读它
第一个步骤的程序如下图所示:
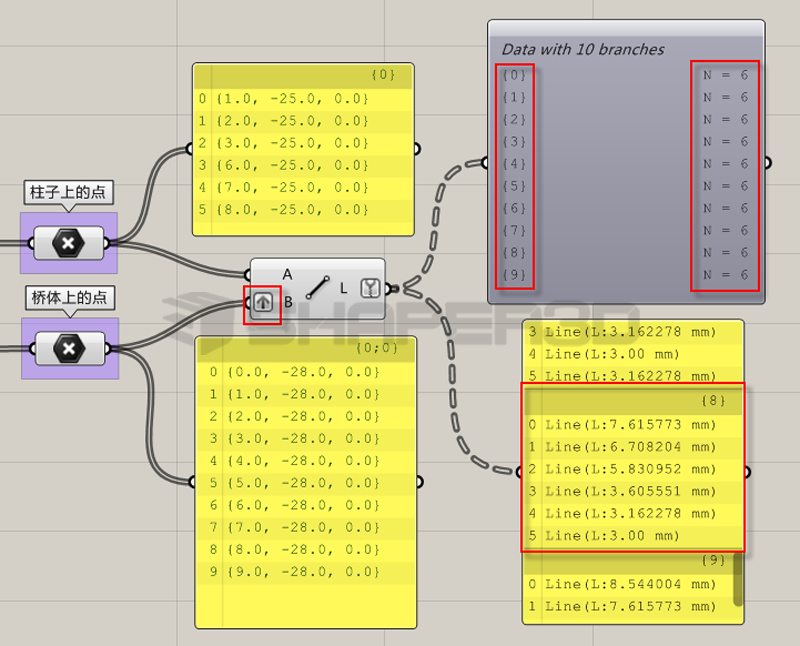
程序处理细节:为了保证输出结果是分组树形结构,因此根据GH的数据对应法则,必须把B端的数据做Graft处理,这样数据的对应方式就变成每个点和顶部的六个点做数据对应连接线。
< 用户应该了解:做Graft之后数据产生什么样的结构变化?为什么要把B端做Graft,而不是把A端做Graft?如果对A端做Graft数据会变成什么样的数据结构?为什么需要这样的数据结构?>
接下来的程序实现第二个步骤:从得到的60根条线中,找出连接每个点的6条线中最短的一根。
这个功能从编程逻辑角度思考可以这样解决:首先对每个点的六条线的长度做从小到大的排序,然后从中挑第一条线,因为第一条线必定是每个点的六条线中最短的一根。这部分并不涉及数据结构的处理,理解工具运作的原理就可以做出来,程序如下。
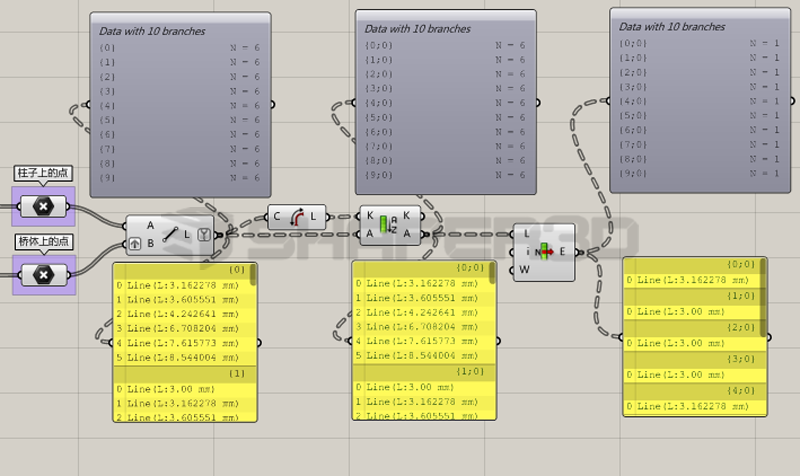
效果如下图,每条线都是底部的每个点与顶部6个点中最近的一个点的连线:
在这个例子中,如何控制程序将输出的60根线使用树形结构做正确的归属管理是程序实现正确连线效果的关键。
综合优化的方案
在实际设计中,很多时候采用的解决方案都不是那么极端的,例如第一个方案安全性自然是最好,但是因为连线很多意味着实际项目中钢缆也必须使用很多因此造价很贵。而第二种方案虽然造假最便宜,但是因为每个桥体上的固定点子只有一根钢缆固定,因此安全性最差。而且可以试想如果其中有一根柱子断了,那么整个桥就有一半的区域完全没有支撑,因此很可能整个桥立马就垮了。所以有时候我们会综合造价、成本等因素来考虑解决方案。
因此从加强安全性角度考虑可以使每个桥体的固定点都有2根钢缆固定,且两根钢缆分别连接不同的立柱。再从造价和力学角度考虑让每根钢缆连接对应的立柱中最短的一个点,这样可以在安全性和造价方面获得一个不错的平衡。
因此这个设计的要求就是:
找出底部10个点的每个点分别跟两个立柱连接的3根线中最短的一根。
这个设计从逻辑上来讲其实和第二个方案比较接近,区别在于第二个设计仅仅要求找出每个点的6个连线中最短的一个,而这个设计要求还需将每个点的6根线按照立柱的归属分成2组,然后再找出每一组中的最短的线。因此输出的60根线应该是按照如下的树形结构管理:
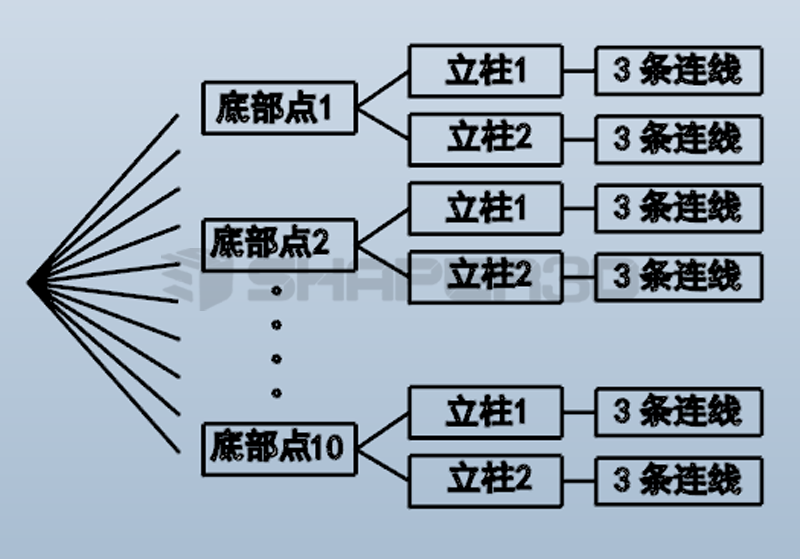
在明确希望得到的数据结构后,来看程序:
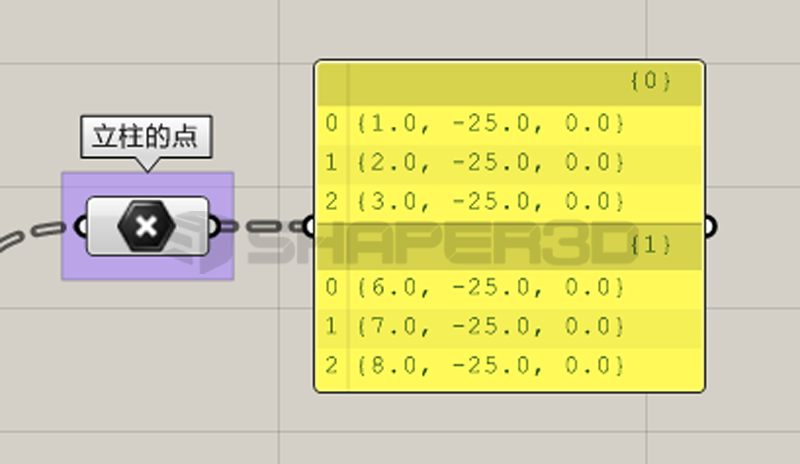
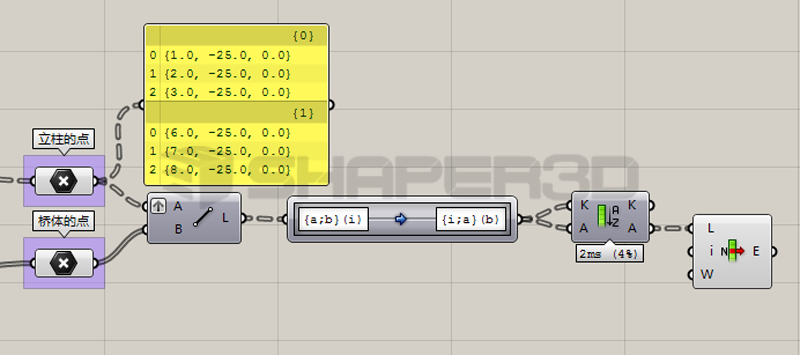
首先在程序的立柱点输入端输入的数据必须按照立柱归宿做树形结构的管理,两个分支对应两个立柱,每个分支里面3个数据对应每个立柱的三个固定点。
<立柱的树形数据结构依赖于前端的程序对应生成>
在接下来的连线程序部分会遇到数据对应方面的控制问题,当前程序部分结构如下:
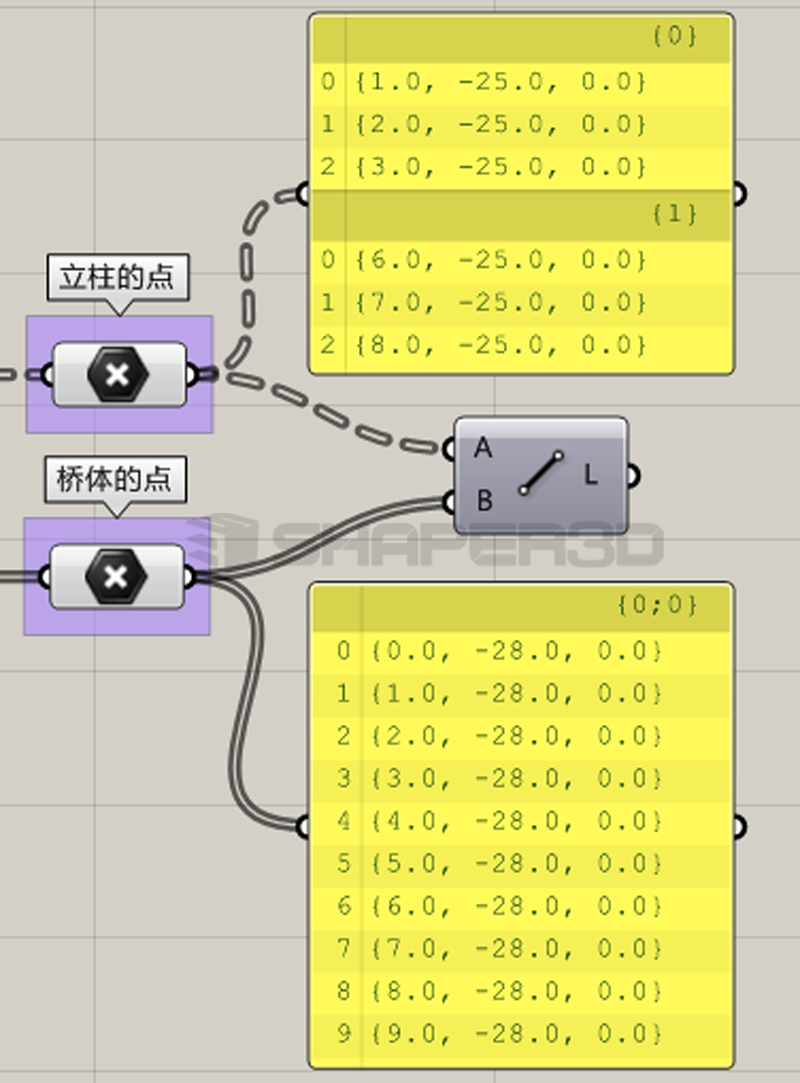
现在A和B组数据的结构与之前不同(并非单分支对单分支),按照GH的数据对规则来看,事实上这里无论怎么调整都不可能直接得到我们要的数据结构。<想想为什么>
因此我们的考虑就是退而求其次:如果没有办法直接得到60根线的:10个点—2个立柱—-3根线 的树形结构方式,那么我也可以接受其他的树形结构管理方式,只要60跟线的数据没有混在一起,我们就可以在后面做树形结构的的调整。
因此在这里我们的考虑变成:怎么样处理程序让得到的60根线的树形结构可以体现出:分别属于桥体10个点、分别属于2个立柱、分别属于立柱的3个固定点的结构?也即是树形结构中必须体现出:10,3,2的结构,无论顺序如何。
<这里根据排列原则有六种树形结构是符合要求的>
当前的程序从输入数据的树形结构来分析唯一可以做到这个效果的方法就是:将A组的数据做Graft,<用户可以去思考为什么其他方式都不可以?>如下图所示。
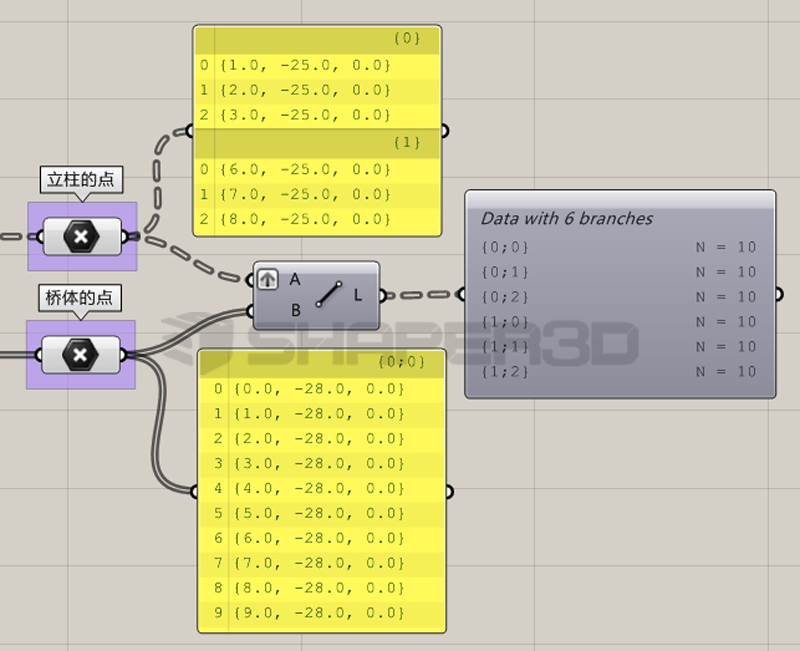
读一下输出的数据接结构,我们看到目前的数据结构是这样管理的:
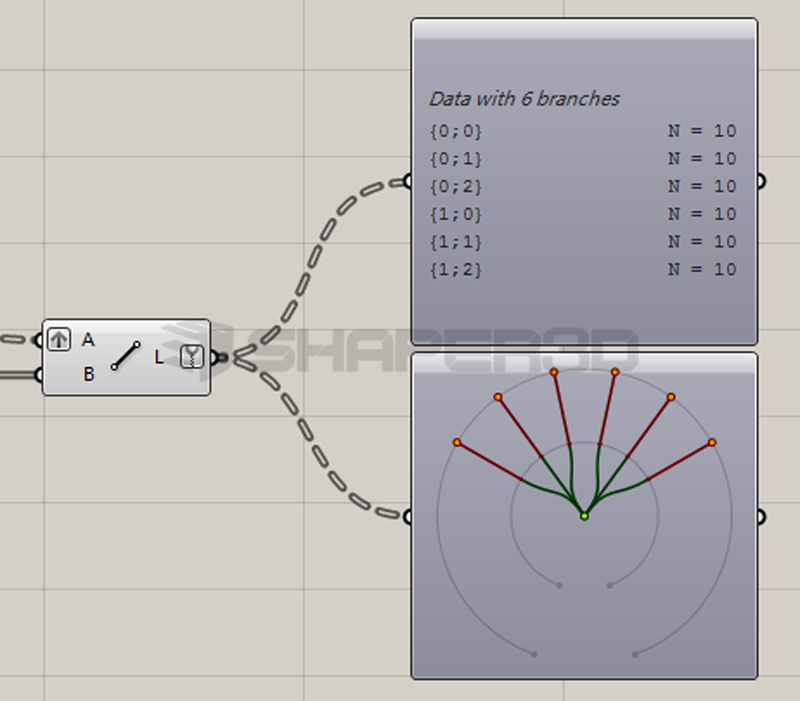
其数据管理逻辑是:
这个树形结构可以体现2,3,10的结构,因此他是合理的。但我们希望树形结构管理是这样:底部10个点中的每个点分别于两个立柱的3条线中最短的一条。因此数据结构应该是:
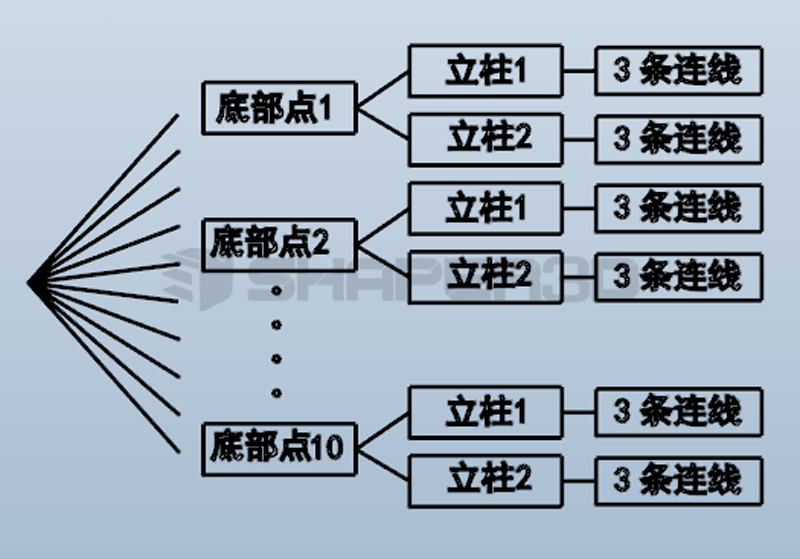
因此接下来我们需要在GH中把当前的树形结构做对应调整:
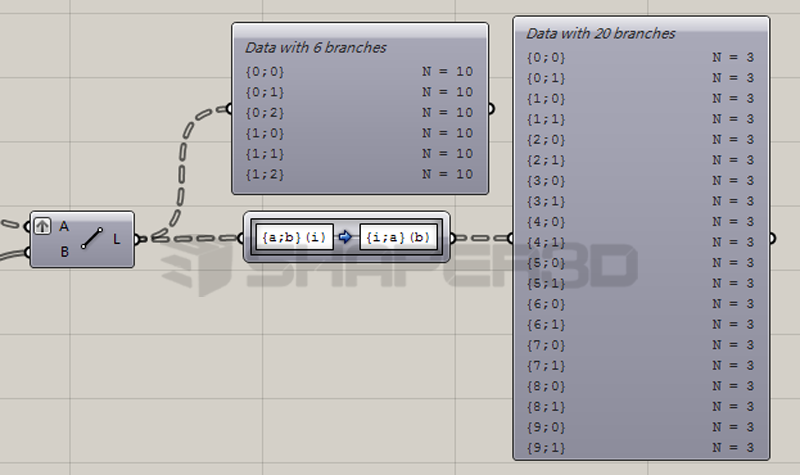
<在这里为调整树形结构使到的工具是Path Mapper,Path Mapper在调整树形结构方面有非常多的用途,但是如何灵活运用它依赖于用户必须能看懂树形结构,读懂树形结构代表的数据管理逻辑,还必须明确自己需要的树形结构是什么样,才能配合Path Mapper做对应的调整。>
一旦树形结构调整正确了,后面的部分就很容处理了,跟之前的部分完全一样:对个分支中的三条线的长度做从小到大的排序,根据排序把对应第一条线跳出来即可。完整程序如下。
可以看到,虽然整个程序编写过程涉及的树形管理的理解和控制需要非常多的思考,但是写出来的程序是很简单的。
效果如下图所示:
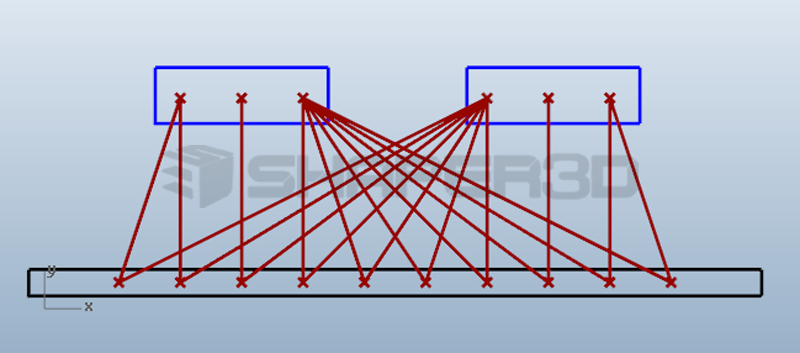
因为程序本身可以处理立柱点输入端的多分枝数据结构,因此对于更加复杂的设计,例如我们需要将立柱数量变成5个,仅仅需要从输入端将对应的5个分支的数据输入即可,程序不需要做任何修改,仍然是简单的结构但是可以处理复杂的数据,如下图所示:
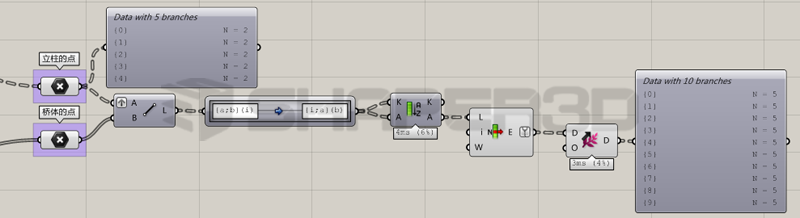
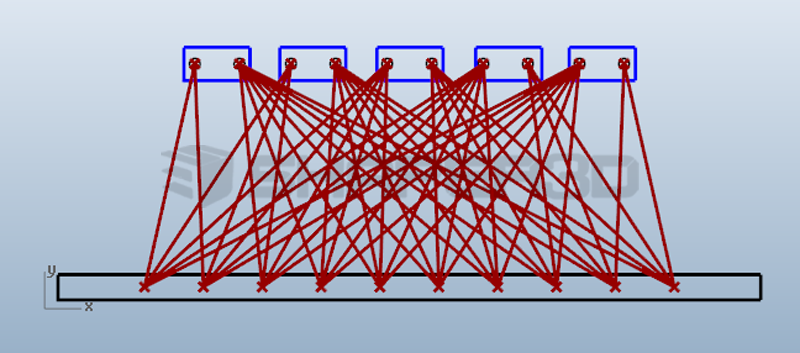
题外话
该部分并不是这个范例中的教学,而是花点篇幅解释一种我们认为不够好的编程思路。虽然这也是一种方法。
例如刚才我们提到的第三种方案:
找出底部10个点的每个点分别跟两个立柱连接的3根线中最短的一根。
遇到这种需要处理复杂的树形结构的程序的时候,我们经常见到这种做法:
1,程序仅考虑处理单根柱子的情况,这样程序会较为简单,程序如下:
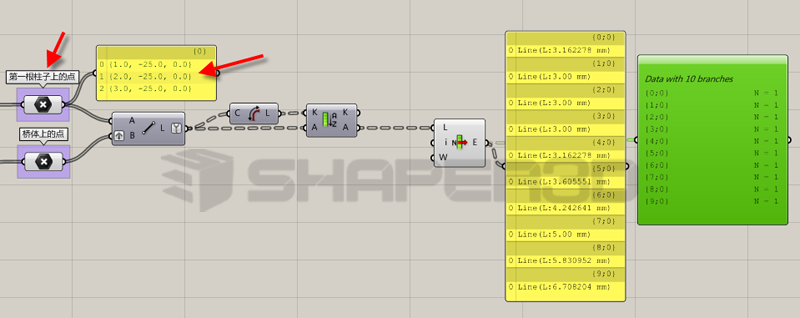
效果如下
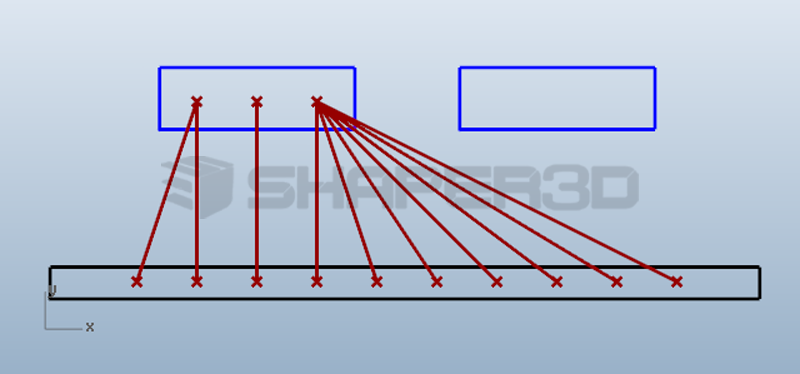
这个程序几乎可以沿用最简化方案的程序,但输入仅仅是3个点(第一根柱子)。
当需要处理多根立柱的数据的时候,将整个程序复制一个,输入端接入另一根柱子的3个点,最后再把数据合并在一起如下图所示。
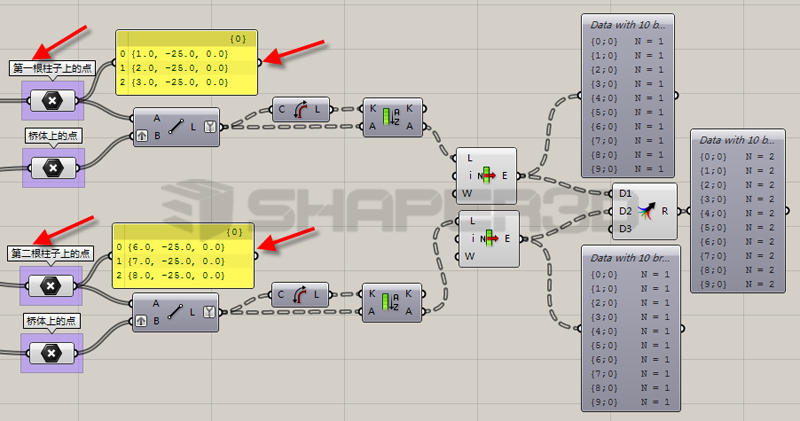
这种做法虽然也可以做到本例中的效果,但是其的本质是用多个一模一样的程序并排分别处理不同立柱中的数据,然后再把每个程序得到的数据合并在一起。
这种做法如果要说好处,应该是可以少费一点脑力把。但是缺点是很明显的,如果柱子数量较多,那么就需要对应数量的完全一样的程序来并排处理,程序会因此变得很复杂,不利于修改和管理程序,程序执行效率也会变得比较低。例如前例中最后提到的:如果设计变动成5跟立柱,那么程序就必须复制出5个一模一样的,分别处理每根跟立足的数据,如下图所示:
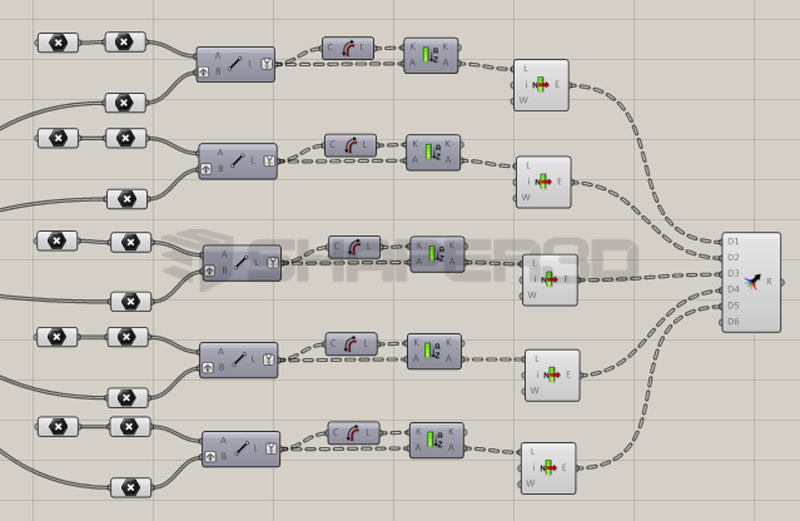
另外这种方式还有一个致命缺点:如果柱子数量本身是一个设计中考虑的变量,那么如果柱子数量发生变动,每次都必须手动修改程序,否则程序运行就会出错。
也即是说,这种方法是因为程序无法处理输入端的树形结构数据,因此把数据结构拆开让多个程序分别处理,因此这种程序往往显得不够“聪明”,它不能适应输入的数据分支结构发生变化的情况。
我们希望学员可以掌握能够处理复杂的树形结构的程序的方法,写出高效而聪明的程序辅助设计。
Dixon
2012-5-30
点击查看 原厂 2013 Grasshopper参数化设计课程 详细内容
如果您对这个教学感兴趣或者有疑问请至http://bbs.rhino3d.asia/thread-20271-1-1.html讨论
『Shaper3d 教学网』原创教程 ,转载请注明来源与作者。


 Rhino原厂面授课程
Rhino原厂面授课程












 专题教学
专题教学




