
分享使用Rhino WIP 建构韩国iArc Architects设计的Tri-bowl 建筑造型过程……
由韩国iArc Architects 建筑事务所设计的这座Incheon Tri-bowl ,位于韩国仁川松岛中央公园,2010年竣工后成为一座标志性建筑。


这座建筑像三只大小不一的碗相互融合而成,以下图片是建筑的概念设计草图。
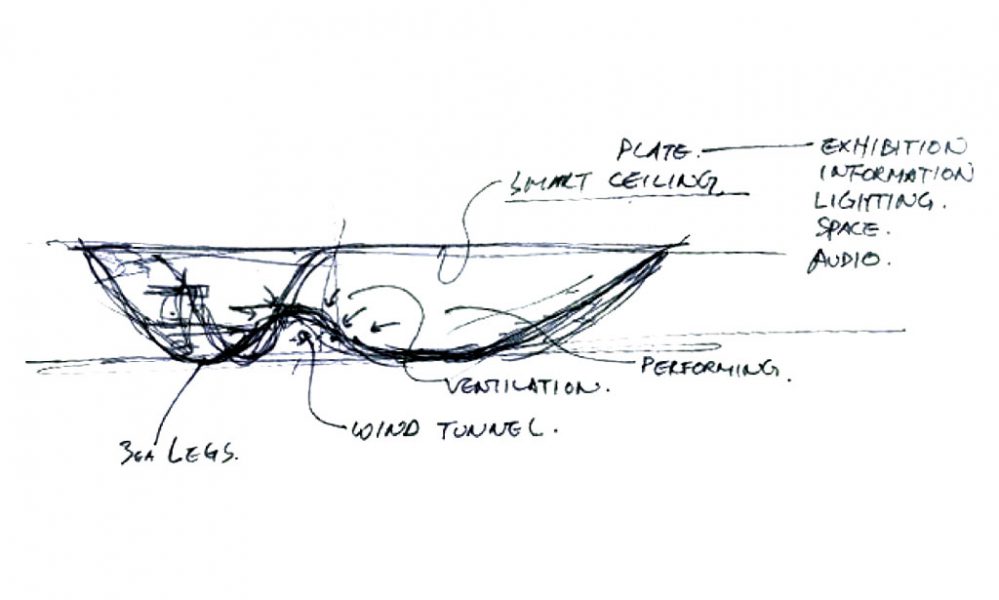
▲以上图片来自:http://iarc.net/
当设计师遇到这类异形建筑概念设计时,该入手建构起3D模型呢?
根据此造型的结构,我们将利用Rhino WIP 的细分指令来快速建立起3D模型,因此以下分享的重点是建构方法而不是把这建筑一模一样“还原”。
软件版本: Rhino WIP 7.0.20071.5245, 03/11/2020
01 从平面开始
1.1 从图片可以看到该建筑的顶部是平的,我们就从这个平面形状入手,使用Curve 指令画出四个封闭的轮廓线。外轮廓曲线是建筑的顶部,内部三个图形是建筑物的底部轮廓,见下图:

提示: 在能满足轮廓精度前题下以尽量少的控制点来绘制曲线。
1.2 利用这组平面曲线,使用PlanarSrf 指令生成平面。

02 重拓扑构建四边网格
上一步,我们建构出一张轮廓平面,那如何令这平面变成立体造型?
接下来我们将使用SubD 方式来建构立体造型:
Rhino WIP 中一个指令-QuadRemesh ,它能基于这张轮廓平面秒算出我们需要的SubD曲面。
2.1 先选取轮廓平面,在SubD Tools 工具条中点击QuadRemesh 指令后会弹出参数设置面板,按下图设定所得到的结果:
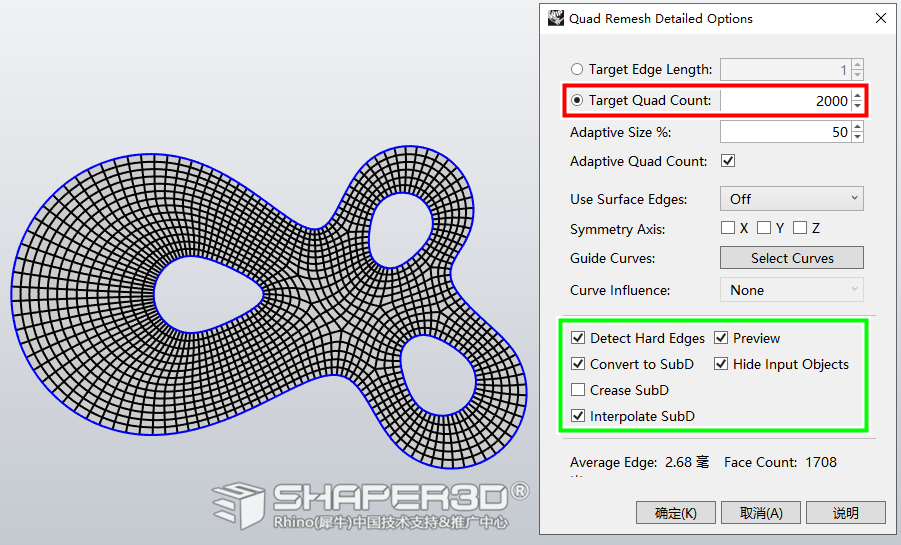
提示:
● Target Quad Count 设定目标四角网格数方式来拟合出细分曲面
● Convert to SubD 输出为细分曲面
● Preview 预览结果
● Hide Input Objects 方便观察结果
● Interpolate SubD 令细分面连轮缘可吸附至目标边缘的最近点
按以上的选项和参数设定,生成细分曲面能很好地拟合到目标曲面去,如下图所示:
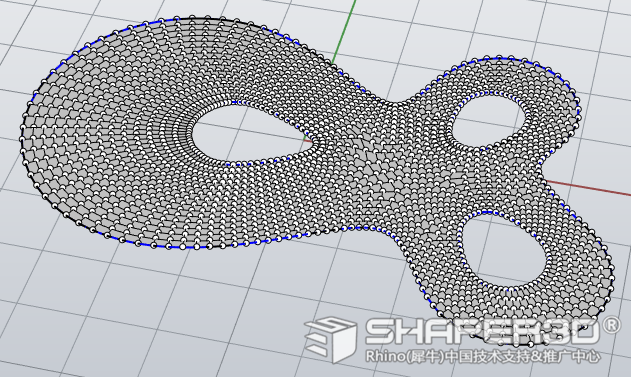
但这种面数的细分曲面是不适合进行手工调形了,因此需要对Target Quad Count 参数进行调整,在数量与拟合精度中找出最适合的参数。
2.2 对Target Quad Count 参数由默认的2000下调至200看看,得到以下效果:
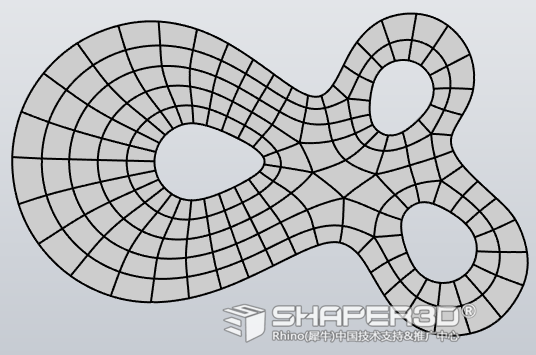
面数下调后,虽然边缘的拟合误差会增大,但有利于后期的手工调整基础造型上。
提示:
● Quad Remesh 会根据目标外形结构计算出合适的面数,因此Target Quad Count 输入的参数与最终面数将有一定的差异。
● 最终面数见面板右下角Face Count 显示,如下图:
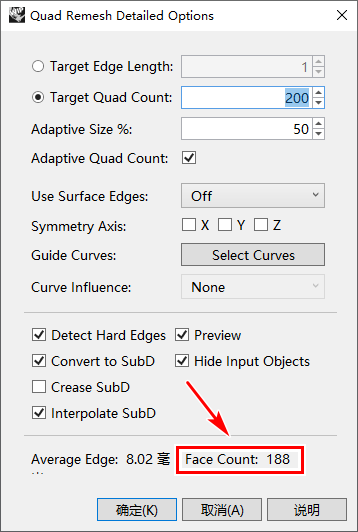
2.3 尝试继续降低面数,Target Quad Count为120,如下图:
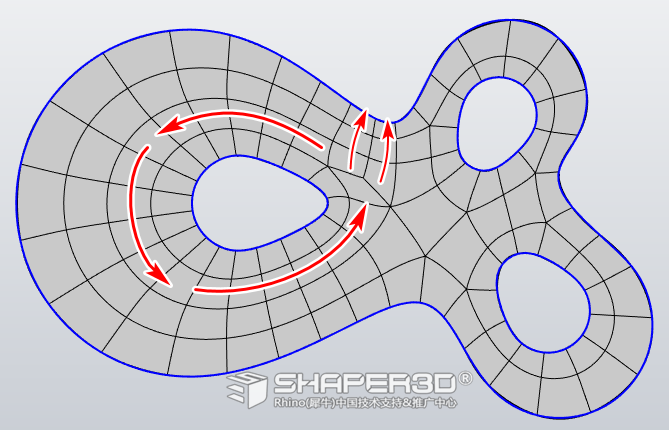
提示: 细分曲面局部边缘与目标边缘存在的间隙可以通过手工调整控制点来进行改善。
这细分面的面数适合手工调整了,但上图红色箭头所示面的走向出现分叉结构,我们希望此处的面是循环结构,如何更改呢?
2.4 在需要保持循环结构的地方先绘制引导曲线,见下图:
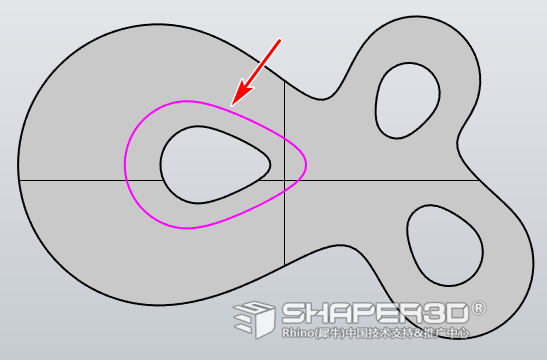
2.5 再次运行QuadRemesh ,点击面板上的“Select Curves”按钮来选取引导曲线,如下图:
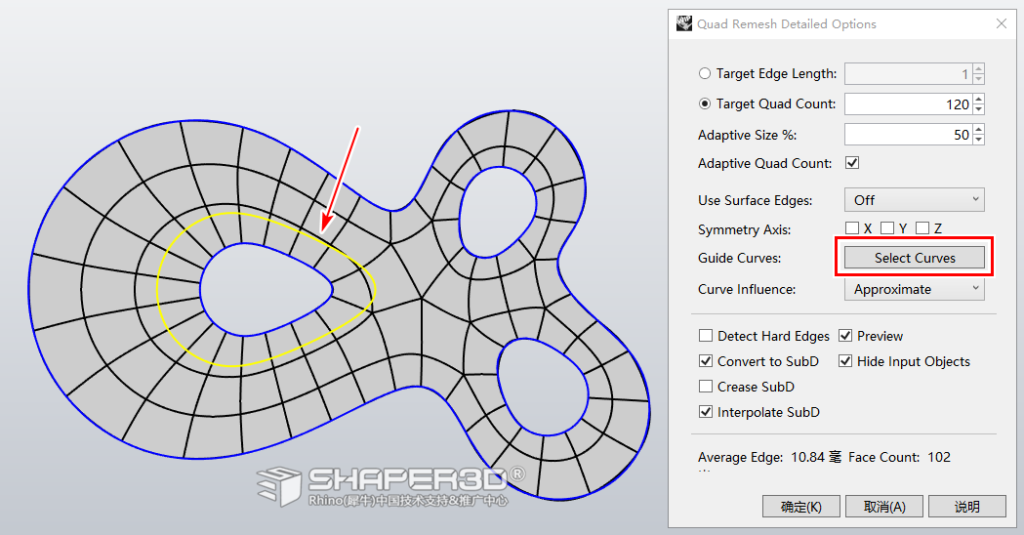
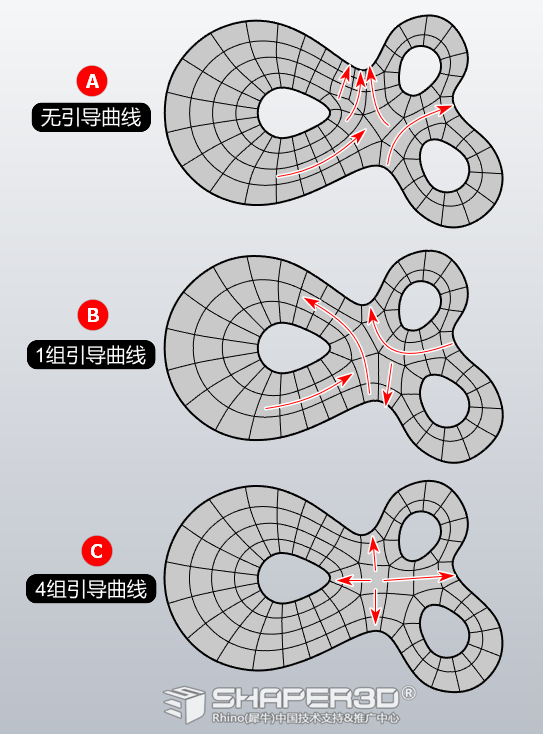
下图是加入引导曲线与没引导曲线的结果对比:
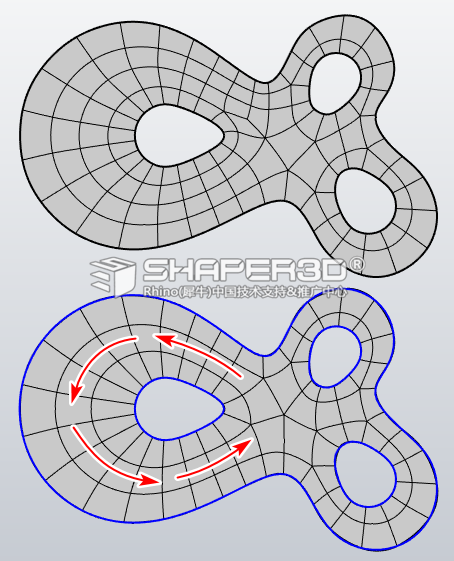
加入引导线后的布线更趋工整、合理,继续尝试加入下图所示的引导曲线后得到的结果。
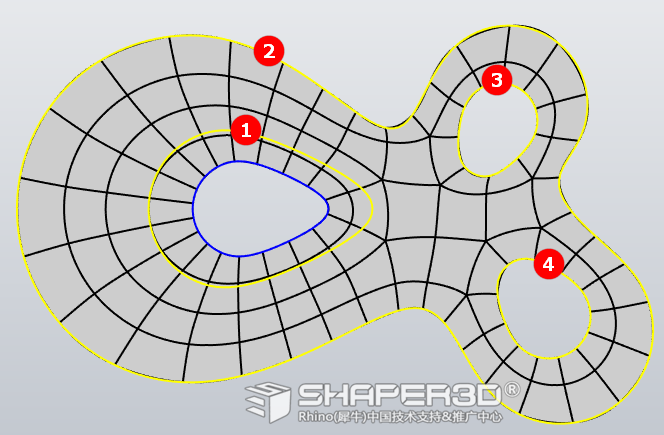
为了方便作比较,见以下图:
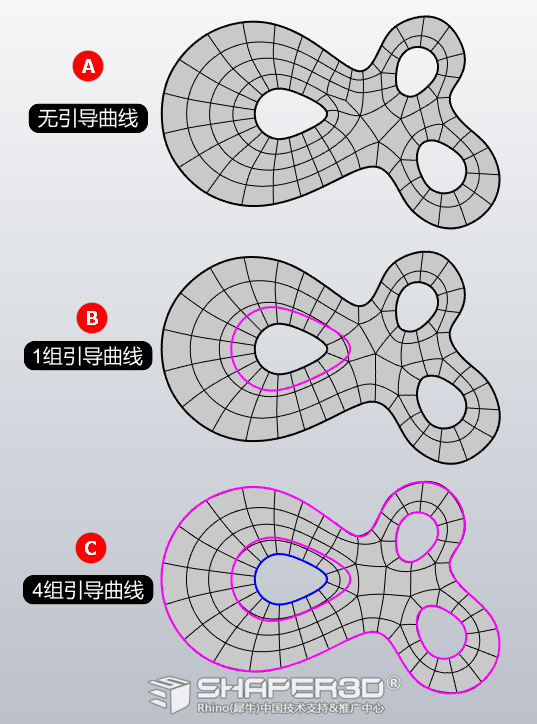
很明显C结果是最合适的,原因是其拓扑结构最合理,看以下这对比分析图:
03 手工修改分面
3.1 QuadRemesh 帮我们算出了一个近乎完美的拓扑结构,根据 Tri-bowl建筑造型特点,需要对分面进行手工调整优化,看以下操作:
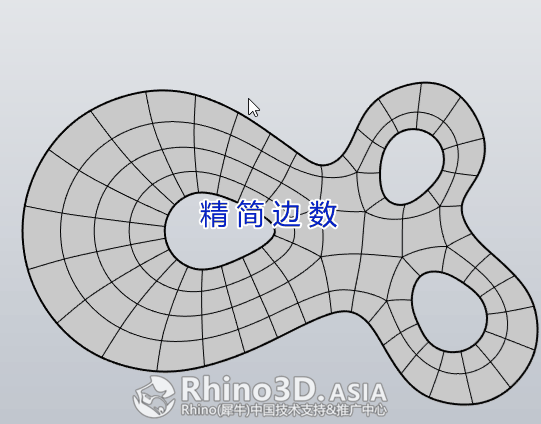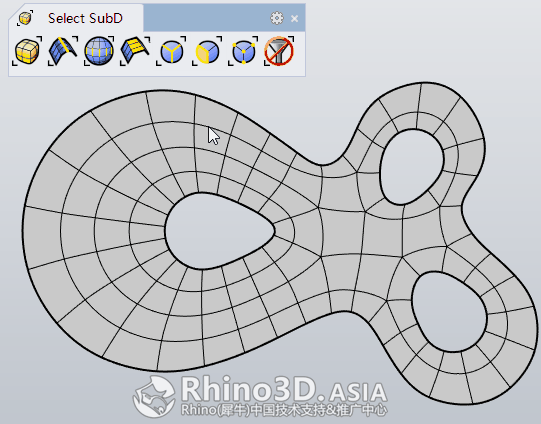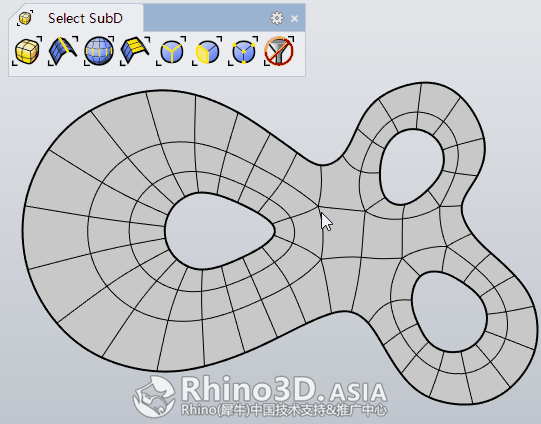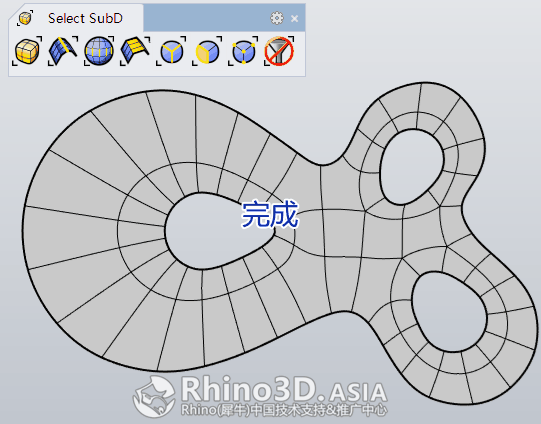
提示: 目前Rhino WIP 版提供了Select SubD选取工具,如最常用的选取顶点、边、面、物件等,见下图:
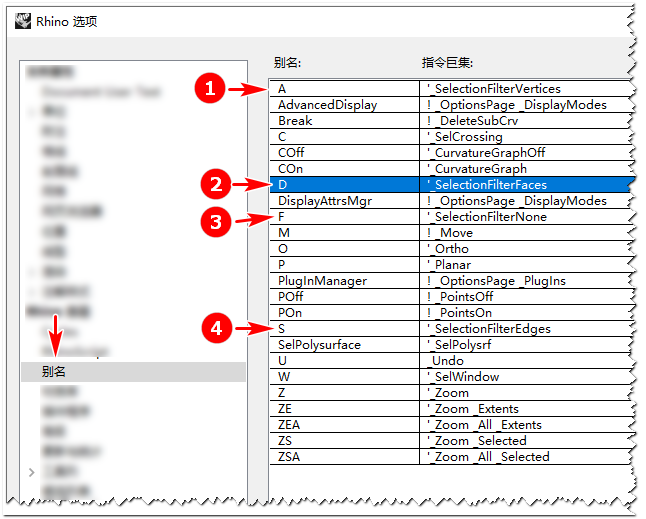
除了点击按键进行选取外,更推荐自订快捷键来选取,如键盘的A S D F 键对应顶点、边、面、对象,设定的方法如下:
删掉边后出现下图的5边面:
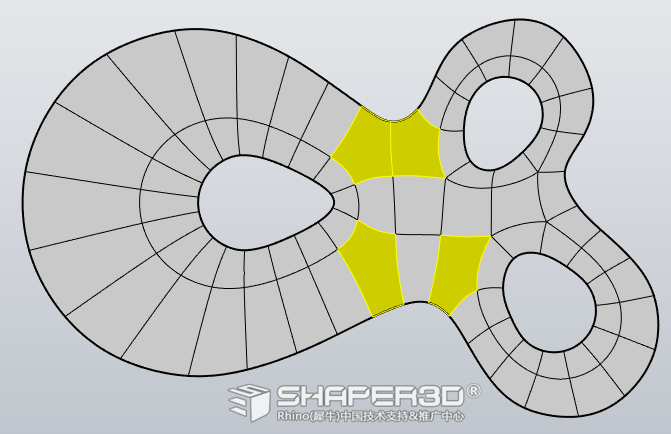
3.3 使用InsertPoint 指令对分面进行以下修改:
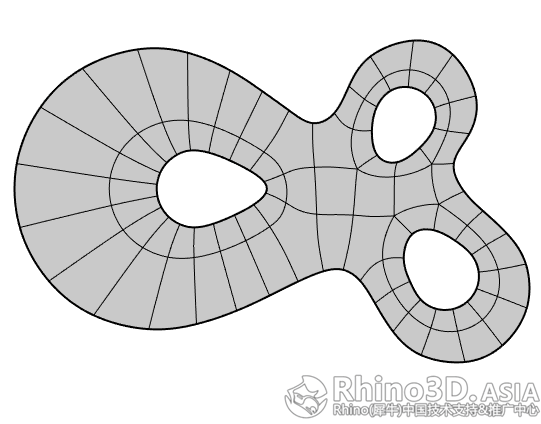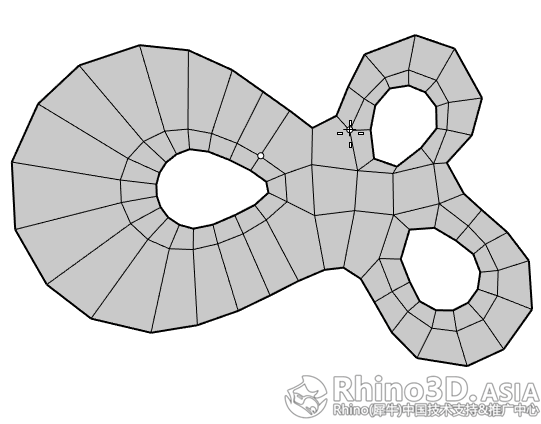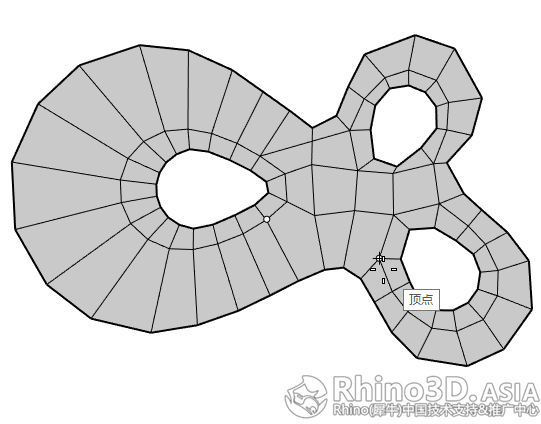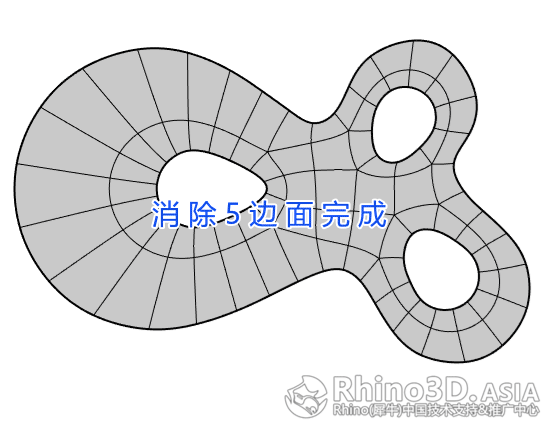
通过插入新的边后,原来的5边面被划分成四边面结构。
04 调整基础造型
经过上面操作后,我们得到一张平面状的细分曲面,接下来通过手工拖动边或顶点来使它变成立体造型 。
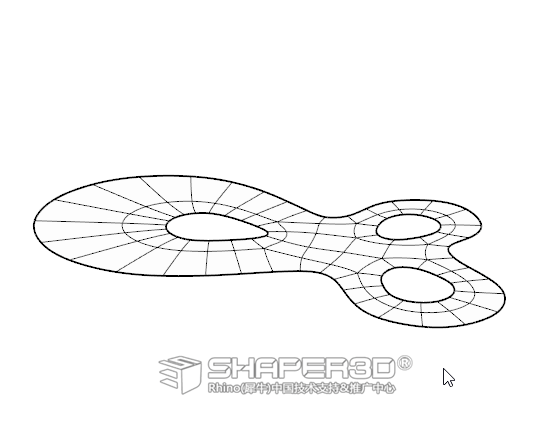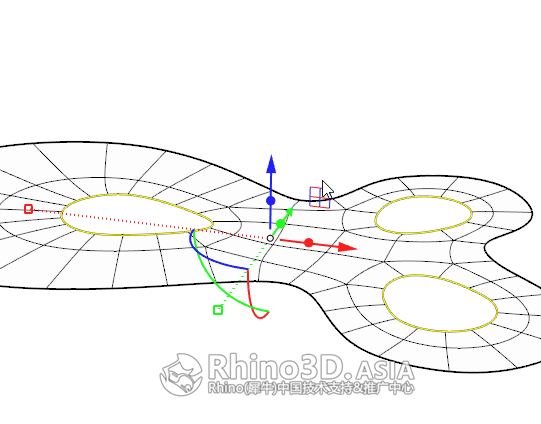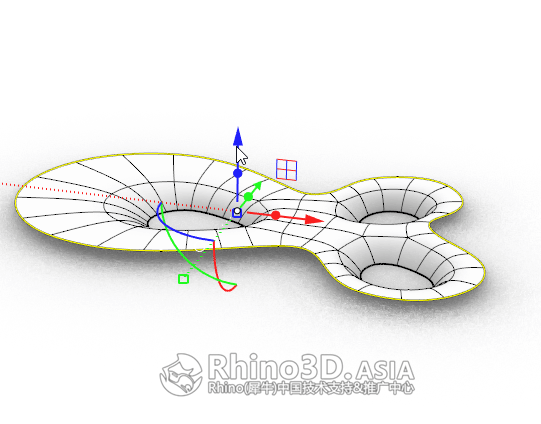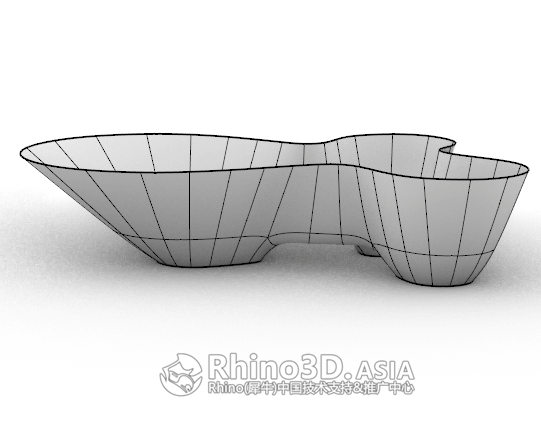
4.2 在顶点选取模式下,调整分面如下图:
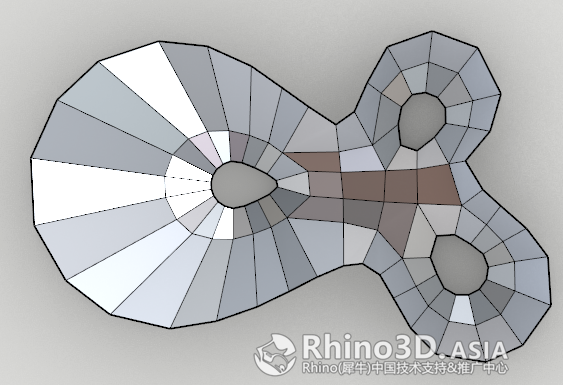
经过简单快速调整后,我们就能得到以下这个效果,此时Tri-bowl 建筑主体已完成。
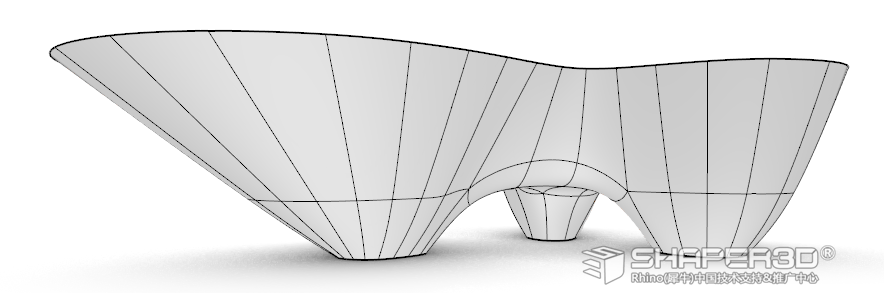


05 转成NURBS 加工细节
接下来用ToNurbs 指令把调整好的细分曲面转成NURBS多重曲面,见下图:
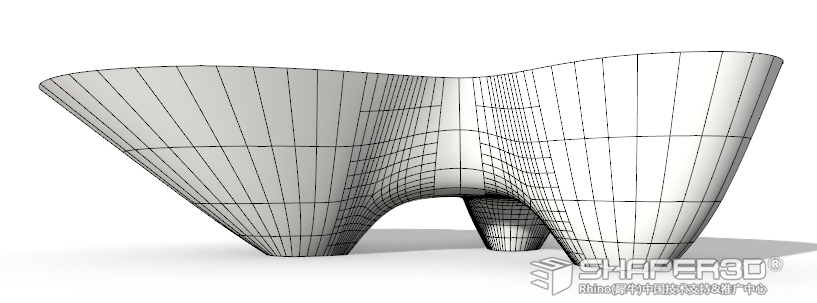
5.1 在主体上分割出墙幕部分,见下图:
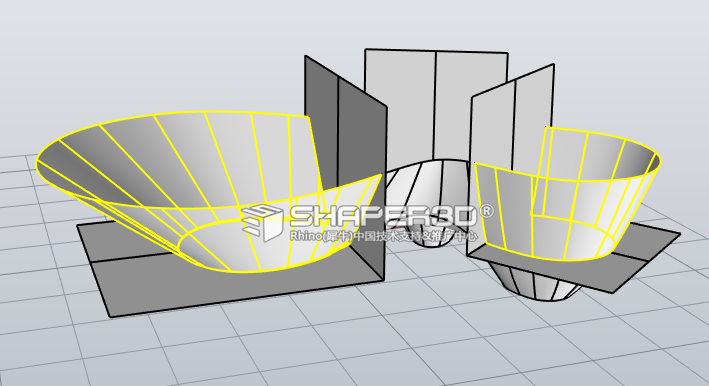
5.2 重建三块墙幕的曲面:
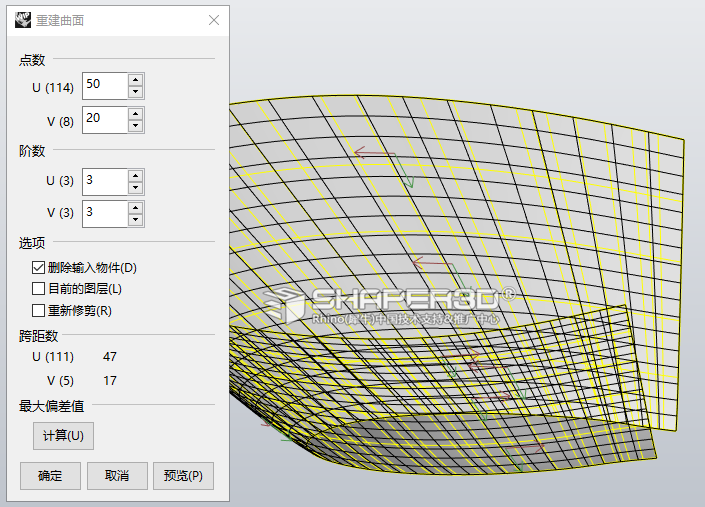
其余细节加工都很简单,在此略去。最后Tri-bowl 建筑完成后的效果



当遇上异形建筑的概念设计阶段时,Rhino 的细分曲面混合NURBS 建模可以帮你快速精确实现设计。
本教学完!

 Rhino原厂面授课程
Rhino原厂面授课程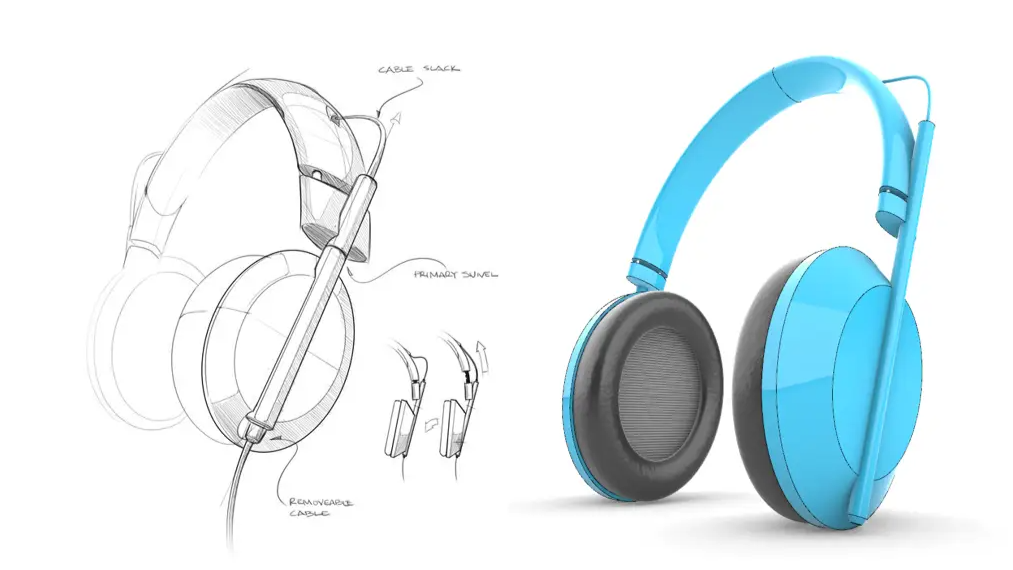












 专题教学
专题教学




